corCTF 2022 writeup

corCTF 2022

---

tadpole

tadpoles only know the alphabet up to b... how will they ever know what p is?
添付ファイル：tadpole.py, output.txt

#tadpole.py
from Crypto.Util.number import bytes_to_long, isPrime
from secrets import randbelow

p = bytes_to_long(open("flag.txt", "rb").read())
assert isPrime(p)

a = randbelow(p)
b = randbelow(p)

def f(s):
    return (a * s + b) % p

print("a = ", a)
print("b = ", b)
print("f(31337) = ", f(31337))
print("f(f(31337)) = ", f(f(31337)))

a =  7904681699700731398014734140051852539595806699214201704996640156917030632322659247608208994194840235514587046537148300460058962186080655943804500265088604049870276334033409850015651340974377752209566343260236095126079946537115705967909011471361527517536608234561184232228641232031445095605905800675590040729
b =  16276123569406561065481657801212560821090379741833362117064628294630146690975007397274564762071994252430611109538448562330994891595998956302505598671868738461167036849263008183930906881997588494441620076078667417828837239330797541019054284027314592321358909551790371565447129285494856611848340083448507929914
f(31337) =  52926479498929750044944450970022719277159248911867759992013481774911823190312079157541825423250020665153531167070545276398175787563829542933394906173782217836783565154742242903537987641141610732290449825336292689379131350316072955262065808081711030055841841406454441280215520187695501682433223390854051207100
f(f(31337)) =  65547980822717919074991147621216627925232640728803041128894527143789172030203362875900831296779973655308791371486165705460914922484808659375299900737148358509883361622225046840011907835671004704947767016613458301891561318029714351016012481309583866288472491239769813776978841785764693181622804797533665463949

modulusを求める問題です。0 mod pとなる式を二つ作りgcdを取ります。今回はgcdがそのままmodulusとなりました。

#solver.py
import math
from Crypto.Util.number import *
a =  (中略)
b =  (中略)
f =  (中略) #f(31337)
ff =  (中略) #f(f(31337))

print(long_to_bytes(math.gcd(a*31337+b-f,a*f+b-ff)))

corctf{1n_m4th3m4t1c5,_th3_3ucl1d14n_4lg0r1thm_1s_4n_3ff1c13nt_m3th0d_
f0r_c0mput1ng_th3_GCD_0f_tw0_1nt3g3rs}

---

luckyguess

i hope you're feeling lucky today
nc be.ax 31800
添付ファイル：luckyguess.py

#luckyguess.py
#!/usr/local/bin/python
from random import getrandbits

p = 2**521 - 1
a = getrandbits(521)
b = getrandbits(521)
print("a =", a)
print("b =", b)

try:
    x = int(input("enter your starting point: "))
    y = int(input("alright, what's your guess? "))
except:
    print("?")
    exit(-1)

r = getrandbits(20)
for _ in range(r):
    x = (x * a + b) % p

if x == y:
    print("wow, you are truly psychic! here, have a flag:", open("flag.txt").read())
else:
    print("sorry, you are not a true psychic... better luck next time")

線形合同法のような形でr回計算した値を予想します。rが20bitと小さい値だ、と思いましたが1/rを引くまで回すのは…。

x = ax + b mod p となるxを渡せば何回計算しようとも同じ値になります。

x = ax + b mod p
(a-1)x = -b mod p
x = -b/(a-1) mod p

#solver.py
from Crypto.Util.number import *
import socket

# --- common funcs ---
def sock(remoteip, remoteport):
    s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
    s.connect((remoteip, remoteport))
    return s, s.makefile('rw')

def read_until(f, delim='\n'):
    data = ''
    while not data.endswith(delim):
        data += f.read(1)
    return data

    

HOST, PORT = "be.ax", 31800

p = 2**521 - 1

s, f = sock(HOST, PORT)
a = int(read_until(f).split()[-1])
b = int(read_until(f).split()[-1])
x = ((p-b) * inverse(a-1,p))%p

read_until(f,"point: ")
s.send(str(x).encode()+b"\n")
read_until(f,"guess? ")
s.send(str(x).encode()+b"\n")
flag = read_until(f).strip()
print(flag)

corctf{r34l_psych1c5_d0nt_n33d_f1x3d_p01nt5_t0_tr1ck_th15_lcg!}

---

exchanged

you could make an exchange out of this
添付ファイル：exchanged.py, output.txt

#exchanged.py
from Crypto.Util.number import *
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from hashlib import sha256
from secrets import randbelow

p = 142031099029600410074857132245225995042133907174773113428619183542435280521982827908693709967174895346639746117298434598064909317599742674575275028013832939859778024440938714958561951083471842387497181706195805000375824824688304388119038321175358608957437054475286727321806430701729130544065757189542110211847
a = randbelow(p)
b = randbelow(p)
s = randbelow(p)

print("p =", p)
print("a =", a)
print("b =", b)
print("s =", s)

a_priv = randbelow(p)
b_priv = randbelow(p)

def f(s):
    return (a * s + b) % p

def mult(s, n):
    for _ in range(n):
        s = f(s)
    return s

A = mult(s, a_priv)
B = mult(s, b_priv)

print("A =", A)
print("B =", B)

shared = mult(A, b_priv)
assert mult(B, a_priv) == shared

flag = open("flag.txt", "rb").read()
key = sha256(long_to_bytes(shared)).digest()[:16]
iv = long_to_bytes(randint(0, 2**128))
cipher = AES.new(key, AES.MODE_CBC, iv=iv)
print(iv.hex() + cipher.encrypt(pad(flag, 16)).hex())

p = 142031099029600410074857132245225995042133907174773113428619183542435280521982827908693709967174895346639746117298434598064909317599742674575275028013832939859778024440938714958561951083471842387497181706195805000375824824688304388119038321175358608957437054475286727321806430701729130544065757189542110211847
a = 118090659823726532118457015460393501353551257181901234830868805299366725758012165845638977878322282762929021570278435511082796994178870962500440332899721398426189888618654464380851733007647761349698218193871563040337609238025971961729401986114391957513108804134147523112841191971447906617102015540889276702905
b = 57950149871006152434673020146375196555892205626959676251724410016184935825712508121123309360222777559827093965468965268147720027647842492655071706063669328135127202250040935414836416360350924218462798003878266563205893267635176851677889275076622582116735064397099811275094311855310291134721254402338711815917
s = 35701581351111604654913348867007078339402691770410368133625030427202791057766853103510974089592411344065769957370802617378495161837442670157827768677411871042401500071366317439681461271483880858007469502453361706001973441902698612564888892738986839322028935932565866492285930239231621460094395437739108335763
A = 27055699502555282613679205402426727304359886337822675232856463708560598772666004663660052528328692282077165590259495090388216629240053397041429587052611133163886938471164829537589711598253115270161090086180001501227164925199272064309777701514693535680247097233110602308486009083412543129797852747444605837628
B = 132178320037112737009726468367471898242195923568158234871773607005424001152694338993978703689030147215843125095282272730052868843423659165019475476788785426513627877574198334376818205173785102362137159225281640301442638067549414775820844039938433118586793458501467811405967773962568614238426424346683176754273
e0364f9f55fc27fc46f3ab1dc9db48fa482eae28750eaba12f4f76091b099b01fdb64212f66caa6f366934c3b9929bad37997b3f9d071ce3c74d3e36acb26d6efc9caa2508ed023828583a236400d64e

Diffie-Hellman鍵共有のような形で、shared = mult(A, b_priv) = mult(B, a_priv) となっており、これが分かればkeyを導出できAES暗号化されたflagを復号できます。A, Bは与えられていることから、a_priv or b_privを求めていきます。

mult関数を見ていきます。線形合同法のような計算をn(=a_priv or b_priv)回行います。nはかなり大きい数字のため、O(n)となる逐次処理では計算が終わりません。ゆえに、mult関数を高速化最適化を行います。

mult(s, 1) = as+b mod p
mult(s, 2) = a(as+b) + b = (a^2)s +ab + b mod p
mult(s, 3) = a((a^2)s+ab+b) + b = (a^3)s + (a^2)b +ab + b mod p
-> mult(s, n) = (a^n)s + (a^(n-1))b + (a^(n-2))b + ... + ab + b = (a^n)s + b(((a^n)-1) / (a-1)) mod p

上記のように、規則性と等比数列の和の公式を使って高速化できる式となりました。ここからn(=a_priv or b_priv)を求めていきます。つまりnの式を作るよう変形すると、

mult(s, n) = A = (a^n)s + b(((a^n)-1) /  (a-1)) mod p
(a-1)A = (a^n)(a-1)s + (a^n)b - b mod p
(as-a+b)(a^n) = (a-1)A + b mod p
(a^n) = ((a-1)A+b) / (as-a+b) mod p

右辺は既知の変数のみで構成されているので計算できます。あとは、(右辺の値) = aⁿ mod pとなる値を求める過程だけなのですが、離散対数問題を解くということとなります。

p-1が素因数分解可能かつ小さい素数のみで構成されている場合、Pohlig-Hellman algorithmを用いて離散対数問題を解くことができます。

en.wikipedia.org

p-1を素因数分解してみると、小さい素数のみで構成されていたので、Pohlig-Hellman algorithmを使えそうです。

factorDBで素因数分解

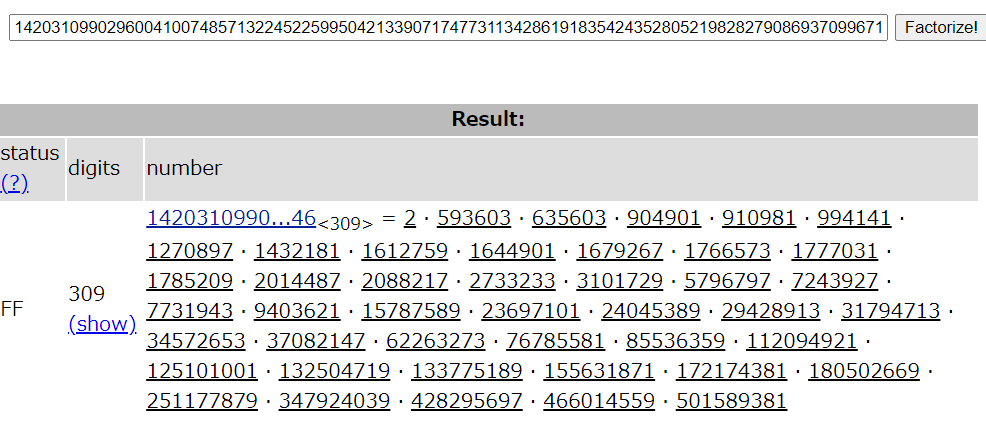
sageのdiscrete_logにはこのアルゴリズムが搭載されているようなので、あとはsageに任せます。

#sage 離散対数問題を解く
print(discrete_log( Mod(右辺値, p), Mod(a, p) )

from Crypto.Util.number import *
import math
import gmpy2
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from hashlib import sha256

p = (中略)
a = (中略)
b = (中略)
s = (中略)
A = (中略)
B = (中略)
enc = (中略)

def mult(s, n):
    deno = inverse(a-1,p)
    t = ((pow(a,n,p)-1)*deno)%p
    return (pow(a,n,p)*s + b*t)%p



An = ((A*(a-1)+b) * inverse((a-1)*s+b,p))%p
Bn = ((B*(a-1)+b) * inverse((a-1)*s+b,p))%p

print(An)
print(Bn)

#---

b_priv = 72294308363142635191285137067271613704518381689222403756427895774621470359587678998089163134800904011887080683864659561441585487866597353332892511005327144670737921076740544522591181991307617152388962472418690715521378068114703790176987564145359661515790454979281591952064634314009219343525018858317272168846

assert mult(s,b_priv) == B

shared2 = mult(A, b_priv)
print(shared2)
key = sha256(long_to_bytes(shared2)).digest()[:16]
iv = bytes.fromhex(enc[:32])
cipher = AES.new(key, AES.MODE_CBC, iv=iv)
print(cipher.decrypt(bytes.fromhex(enc[32:])))

corctf{th1s_lcg_3xch4ng3_1s_4_l1ttl3_1ns3cur3_f0r_n0w}

---

hidE

This RSA encryption service is so secure we're not even going to tell you how we encrypted it
nc be.ax 31124
添付ファイル：main.py

#main.py
#!/usr/local/bin/python
import random
import time
import math
import binascii
from Crypto.Util.number import *

p, q = getPrime(512), getPrime(512)
n = p * q
phi = (p - 1) * (q - 1)

flag = open('./flag.txt').read().encode()

random.seed(int(time.time()))

def encrypt(msg):
    e = random.randint(1, n)
    while math.gcd(e, phi) != 1:
        e = random.randint(1, n)
    pt = bytes_to_long(msg)
    ct = pow(pt, e, n)
    return binascii.hexlify(long_to_bytes(ct)).decode()


def main():
    print('Secure Encryption Service')
    print('Your modulus is:', n)
    while True:
        print('Options')
        print('-------')
        print('(1) Encrypt flag')
        print('(2) Encrypt message')
        print('(3) Quit')
        x = input('Choose an option: ')
        if x not in '123':
            print('Unrecognized option.')
            exit()
        elif x == '1':
            print('Here is your encrypted flag:', encrypt(flag))
        elif x == '2':
            msg = input('Enter your message in hex: ')
            print('Here is your encrypted message:', encrypt(binascii.unhexlify(msg)))
        elif x == '3':
            print('Bye')
            exit()

if __name__ == '__main__':
    main()

UNIXTIMEの小数点以下を切り捨てた整数をシードとし、暗号化の要求があるたびに生成した乱数をeとしています(phiと互いに素でなければ、互いに素になるまで生成する)。flagの暗号文と任意の整数の暗号化を何回でも取得できます。

まず、シードは予測できそうです。ncするタイミングで±10秒あたりを見れば問題なさそうです。

eが1~nの間なので、かなり大きくなる可能性があるのでWiener's Attackかと思って進めていきましたが、e/nが0.96の場合でもうまくいかずdが小さくなってないのでしょう…。何かないかといつもの資料を見ていると、Common Modulus Attackなのでは？となりました。

RSA暗号運用でやってはいけない n のこと #ssmjp from sonickun

www.slideshare.net

Common Modulus Attackは前半で出てくるイメージでしたが、だからといって気付くのが遅いなぁと反省。flagの暗号文を2つ取得し、シードをbrute forceして乱数を得てこの攻撃を行います。

#solver.py
from Crypto.Util.number import *
import socket
import time
import random
import gmpy2

# --- common funcs ---
def sock(remoteip, remoteport):
    s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
    s.connect((remoteip, remoteport))
    return s, s.makefile('rw')

def read_until(f, delim='\n'):
    data = ''
    while not data.endswith(delim):
        data += f.read(1)
    return data

HOST, PORT = "be.ax", 31124
while True:
    try:
        tim = int(time.time())
        s, f = sock(HOST, PORT)
        read_until(f)
        n = int(read_until(f).split()[-1])
        print(f"n = {n}")
        for _ in range(5): read_until(f)
        read_until(f,"option: ")
        s.send(b"1\n")
        c1 = int(read_until(f).split()[-1],16)
        for _ in range(5): read_until(f)
        read_until(f,"option: ")
        s.send(b"1\n")
        c2 = int(read_until(f).split()[-1],16)
        for i in range(20):
            random.seed(tim)
            e_para = []
            for k in range(100):
                e = random.randint(1, n)
                e_para.append(e)

            for i1 in range(len(e_para)-1):
                for i2 in range(i1+1,len(e_para)):
                    e1 = e_para[i1]
                    e2 = e_para[i2]
                    g,s1,s2 = gmpy2.gcdext(e1,e2)
                    g,s1,s2 = int(g), int(s1), int(s2)
                    assert e1*s1 + e2*s2 == g
                    if g == 1:
                        m = (pow(c1,s1,n)*pow(c2,s2,n))%n
                        flag = long_to_bytes(m)
                        if b"corctf" in flag:
                            print(flag)
                            exit()
            tim += 1
    except:
        pass

Wiener's Attackじゃないかと模索している間、この攻撃がpypiで実装されているのを発見して驚いてました(笑)

pypi.org

corctf{y34h_th4t_w4snt_v3ry_h1dd3n_tbh_l0l}

---

generous

Let me introduce you to this nice oracle I found...
nc be.ax 31244
添付ファイル：generous.py

#generous.py
#!/usr/local/bin/python
from Crypto.Util.number import getPrime, inverse, bytes_to_long
from random import randrange

with open("flag.txt", "rb") as f:
    flag = f.read().strip()

def gen_keypair():
    p, q = getPrime(512), getPrime(512)
    n = (p**2) * q
    while True:
        g = randrange(2, n)
        if pow(g, p-1, p**2) != 1:
            break
    h = pow(g, n, n)
    return (n, g, h), (g, p, q)

def encrypt(pubkey, m):
    n, g, h = pubkey
    r = randrange(1, n)
    c = pow(g, m, n) * pow(h, r, n) % n
    return c

def decrypt(privkey, c):
    g, p, q = privkey
    a = (pow(c, p-1, p**2) - 1) // p
    b = (pow(g, p-1, p**2) - 1) // p
    m = a * inverse(b, p) % p
    return m

def oracle(privkey, c):
    m = decrypt(privkey, c)
    return m % 2

pub, priv = gen_keypair()
n, g, h = pub
print(f"Public Key:\n{n = }\n{g = }\n{h = }")
print(f"Encrypted Flag: {encrypt(pub, bytes_to_long(flag))}")
while True:
    inp = int(input("Enter ciphertext> "))
    print(f"Oracle result: {oracle(priv, inp)}")

まずは中のアルゴリズムをまとめていきます。

暗号化
n = ppq
h = g^n mod n
c = g^m × h^r = g^m × (g^n)^r = g^(m+nr) mod n

復号
a = ((c^(p-1) mod p^2)-1) / p
b = ((g^(p-1) mod p^2)-1) / p
m = a × b^(-1) mod p

oracle
公開鍵をくれる
flagの暗号文をくれる
任意の暗号文を復号し、その下位1bitだけ教えてくれる

おそらくflagを1bitずつ求めていって復元するという形になると予想されます。

どっかで見たことあるなぁなんか名前あったなぁという暗号化方式で、自分の記憶を頼りにWaniCTFだったかなとはてなブログを遡ると…見つけました！

WaniCTF'21-spring Crypto Writeup - Attack All Around

暗号化方式は同じで復号oracleも存在しているのですが、この問題はflag以外の暗号文は全て復号してくれるという問題でした。cをflagの暗号文とすると、c' = c² mod nを復号してもらうと2×flagとなり、半分で割ってlong_to_bytes()していました。それにしても、1年前の自分はちゃんと復号される証明までできていたのに今は分からなくて退化してる…。

この問題のflagより、この暗号化方式はOkamoto-Uchiyama cryptosystem(以後、OU)という名前のようです。

Okamoto–Uchiyama cryptosystem - Wikipedia

この名前でググるとほとんどCTFのwriteupなのですが、n=pppとしている問題かこのWaniCTFのものでした。

こちらのwriteupを参考にすると、OUは準同型暗号のようで平文x+yの暗号文はxの暗号文とyの暗号文の積となるようです。

qiita.com

それで2mの暗号文は、f(m+m) = f(m)×f(m) = c×c = c² mod n なのかとようやく理解しました。OUCSはほとんどの方が、m+1の暗号文を作成してサーバに復号させていたようです。

以上より、m' = m//2 の暗号文をどうにか作れないかと式をたくさん書いた紙とにらめっこします。

m / 2 = m × 2^(-1) = m + m + ... + m mod n
c' = c^(2^(-1)) mod n

このようにして、復号するとm/2となる暗号文c'を作成できました。しかしmが奇数である場合についても考える必要があります。mの下位1bitが分かれば次は2bit目です。1bit目が1である場合、(m-1)/2の暗号文を導出すれば2bit目が分かります。

(m-1)/2 = (m-1) × 2^(-1) = (m+(n-1)) × 2^(-1) =  (m+(n-1)) +  (m+(n-1)) + ... +  (m+(n-1)) mod n
c'' : (n-1)の暗号文
c'' = g^(n-1+nr) mod n
c' = (c × c'')^(2^(-1)) mod n

cを復号して下位1bitが0ならm/2の暗号文を作り、下位1bitが1なら(m-1)/2の暗号文を作り、サーバによって暗号文を復号して下位1bitを得る。というのを繰り返してflagを復元していきます。

#solver.py
from Crypto.Util.number import *
import socket

# --- common funcs ---
def sock(remoteip, remoteport):
    s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
    s.connect((remoteip, remoteport))
    return s, s.makefile('rw')

def read_until(f, delim='\n'):
    data = ''
    while not data.endswith(delim):
        data += f.read(1)
    return data

def make_flag(m):
    while len(m)%8:
        m += "0" 
    m = int(m[::-1],2)
    print(long_to_bytes(m))




HOST, PORT = "be.ax", 31244
s, f = sock(HOST, PORT)
read_until(f)
n = int(read_until(f).split()[-1])
g = int(read_until(f).split()[-1])
h = int(read_until(f).split()[-1])
enc = int(read_until(f).split()[-1])



inv2 = inverse(2,n)
n1enc = (pow(g,n-1,n)*pow(h,35,n))%n
enc2 = (pow(g,inv2,n)*pow(h,35,n))%n


flag = ""


for i in range(1000):
    read_until(f,"ciphertext> ")
    s.send(str(enc).encode()+b"\n")
    
    ru = read_until(f)
    bits = ru.split()[-1]
    flag += bits
    if bits == "1":
        enc = (enc*n1enc)%n

    enc = pow(enc,inv2,n)

make_flag(flag)

corctf{see?1_bit_is_very_generous_of_me}

---

corCTF 2021 : corCTF 2021 writeup - Attack All Around

leapfrog面白い問題なのですが、解けなくて悔しい…。