m1z0r3CTF2022 作った問題&writeup
お久しぶりです。
社会人にはなりましたが、m1z0r3CTFには参加できたらなと思い問題を作ってみました(解く方には参加できず)。
※目次が変な感じになってしまい、どう直せばいいか分からず
borderline
めんどくさい計算盛りだくさん
添付ファイル:borderline.zip
#chall1.py from Crypto.Util.number import long_to_bytes import random secret = open("secret.png","rb").read() a = random.randrange(256) b = random.randrange(256) r = random.randrange(256) x = random.randrange(256) enc = 0 for s in secret: enc <<= 8 x = (a*x+b)%r enc += s^x f = open("encrypted_data.dat","wb") f.write(long_to_bytes(enc))
prime connect
prime + prime = prime
添付ファイル:prime_connect.py
from Crypto.Util.number import * def encrypt(st_len,go_len,prime,message): s = 0 l = 1 c = [] while st_len <= go_len: while True: q = getPrime(st_len) qbin = bin(q)[2:] while len(qbin) < st_len: qbin = "0" + qbin next_prime = int(bin(prime)[2:] + qbin,2) if isPrime(next_prime): N = prime * q m = bytes_to_long(message[s:s+l]) e = 101 if prime%e != 1 and q%e != 1: c.append(pow(m,e,N)) prime = next_prime break st_len *= 2 s += l l *= 2 assert len(message) == s return c,N flag = open("flag.txt","rb").read() gen_p = getPrime(16) c,N = encrypt(gen_p.bit_length(),256,gen_p,flag) print(c) # [923347949, 7382279973222128877, 122962146306170765837908848551223454567, 3549519152212014068083700234235160186300219130505299139696292306205464039799, 1527384673643022720120101064151977796913895264858932377772580237410767118686969106391529500139242897405662607203540127567551879700554668904837212450683883] print(N) # 6159034900797898425838526763919325877394844976323736393192254250464963575156530328240421294138007406960476709427205843365628191563244980986067184889098833
borderline 解法
encrypt.pyについて、PNG画像を1バイトずつ暗号化しています。XORを使って暗号化しており、XORするもう一つの値は線形合同法にて決定されます。
ご存知の方も多いとは思いますが、線形合同法には特定の場合において脆弱性が生まれます。 こちらのサイトをよく見るのですが、線形合同法は連続した6個ほどの出力値が分かると、パラメータを算出でき出力値の予想が可能となります。
線形合同法のパラメータを乱数列から求めてみる。 - みつのCTF精進記録
PNGファイルは先頭8バイトが固定であるので、そこから連続した8個の出力値を暗号文とその固定バイトでXORして得られます。
そこから上記のサイトの方法を使って、パラメータを復元します。
その後、他の出力値を計算することで、secret.pngが復元できます。

ということで出題者(私)のgithubに次の問題があります。
GitHub - ksbowler/m1z0r3CTF_2022
import random from Crypto.Util.number import * secret = open("secret.png","rb").read() flag = open("flag.txt","rb").read().strip() assert len(flag)%3 == 0 ex = random.randrange(len(secret)-1) e = bytes_to_long(secret[ex:ex+2]) p = getPrime(256) q = getPrime(256) n = p*q c = [] for i in range(0,len(flag),3): m = bytes_to_long(flag[i:i+3]) c.append(pow(m,e,n)) print(c) # [6298113965475853786056847106208713300642945466885637995557170104494725950616074542425506023987217363886529665397919957618261581053133941027535155746435321, 135028125411958273916880824261545147614327725922209748340303390558194571689687977032589044265126382565916547879777234892642296715526896605761082569309957, 1321747274929612152457518915168588918356514442679554382787182364164828302372180029740168631933681540647333144180952171045221159999310072594994307374026397, 2918560933591924342981380338403848413183651470512194619662681532592047008257668515013412096463534685052633599782673614961906361066771670231196673146753898, 5775447489821919812656223325306418654099675333689382733144673190079859607549709791366025032709099098614570746711061453405145141567455154943434221193937600, 1274850466517264624838781305598541289691584629758963818109637778738466734330749252973718909288129468236472225834841856001947077472220670167226069634313329, 1303782230905842229285244210919421873678385109856332605169575017604438212677510463647334165086069519414714376999894517045356733235945921910952902514007317]
3文字ごと暗号化しており、eはsecret.pngのどこかの連続した2バイト、Nは256bitの素数2つの積となっています。
e, Nは非公開なので、特定していきます。 eはbrute forceしていきつつ、Nを探していきます。 3文字ごと暗号化しており、先頭6文字は"m1z0r3"であるので、
"m1z"^e - 対応した暗号文 "0r3"^e - 対応した暗号文
がNの倍数となります。 この2つのGCDを取ります。GCDの結果、500bit以上になる場合がNの候補となり、今回は1通りしか出ません。
あとはその求めたe, Nを使って、暗号文と同じになる平文をbrute forceで見つけます。
m1z0r3{Time_i5_m0ney}
思いついた経緯
コナンファンなのでtime is moneyは入れたいなと思い、brute force系の問題にしました。
m1z0r3CTF恒例の時間かかる&段階をいくつか踏む問題を作りました。
どこかでPNGファイルの固定8バイトと、線形合同法を組み合わせる問題を見たのでパクりました。
あとは、e, Nすら非公開のRSAがあっても面白いのでは?となり、brute forceできるギリギリのラインで作りました。
prime connect 解法
encrypt関数は以下のような挙動となっています。
・16bitの素数pとflag(とその他諸々)を引数とする ・暗号化𝑖回目 1. pと同じ大きさの素数qを生成する 2. binaryでpとqを繋ぎ合わせた値が素数であれば3に、そうでないなら1に進む 3. e = 101, N = pqとしてRSAで暗号化 4. 暗号化するmはflagの先頭2^(𝑖−1)文字。一度暗号化した文字は暗号化しない。 5. pが256bitとなれば暗号化終わり。 6. p = pとqを繋ぎ合わせた値 7. 暗号化𝑖回目終了、1へ。 ・最後のNと暗号文のリストを公開

ここで、暗号化の3回目まではなんとかなります。 というのも、flagの先頭7文字までは分かっているので、そこから引数で渡された16bitの素数や、1で生成した素数が求められます。 (me-(対応した暗号文) )がNの倍数=p,qの倍数となるので素因数分解すれば分かります。
3回目までのp,qが求まると、4回目での暗号化のpが求まります。また、最後の暗号化におけるpの半分が分かります。 あとは、coppersmith's attack を使って解いていきます。
SageMathを使ってCoppersmith's Attackをやってみる - ももいろテクノロジー
17bitほどbrute forceしないといけないので、時間かけてください笑
m1z0r3{My_1st_coppersmith_quiz}
思いついた経緯
ふと、2進数で素数を繋いでみたらそれも素数になるのかな、なるとしたらどれくらいあるのかな、と思いちょっと動かしてみたらまあまあありそう。 そして、それでNを作ったらなんか脆弱性あるのかなーと考えていたら、pの上位ビット知られちゃいけないのを思い出し今の形を思いつきました。 素数を大きくしていくのでそれに合わせて、暗号化する文字数を増やしていこうと思い、1+2+4=7で"m1z0r3{"のヘッダーが上手く使えるのでは?と。 久しぶりの割には良い問題ができたつもりです笑
corCTF 2022 writeup
tadpole
tadpoles only know the alphabet up to b... how will they ever know what p is?
添付ファイル:tadpole.py, output.txt
#tadpole.py from Crypto.Util.number import bytes_to_long, isPrime from secrets import randbelow p = bytes_to_long(open("flag.txt", "rb").read()) assert isPrime(p) a = randbelow(p) b = randbelow(p) def f(s): return (a * s + b) % p print("a = ", a) print("b = ", b) print("f(31337) = ", f(31337)) print("f(f(31337)) = ", f(f(31337)))
a = 7904681699700731398014734140051852539595806699214201704996640156917030632322659247608208994194840235514587046537148300460058962186080655943804500265088604049870276334033409850015651340974377752209566343260236095126079946537115705967909011471361527517536608234561184232228641232031445095605905800675590040729 b = 16276123569406561065481657801212560821090379741833362117064628294630146690975007397274564762071994252430611109538448562330994891595998956302505598671868738461167036849263008183930906881997588494441620076078667417828837239330797541019054284027314592321358909551790371565447129285494856611848340083448507929914 f(31337) = 52926479498929750044944450970022719277159248911867759992013481774911823190312079157541825423250020665153531167070545276398175787563829542933394906173782217836783565154742242903537987641141610732290449825336292689379131350316072955262065808081711030055841841406454441280215520187695501682433223390854051207100 f(f(31337)) = 65547980822717919074991147621216627925232640728803041128894527143789172030203362875900831296779973655308791371486165705460914922484808659375299900737148358509883361622225046840011907835671004704947767016613458301891561318029714351016012481309583866288472491239769813776978841785764693181622804797533665463949
modulusを求める問題です。0 mod pとなる式を二つ作りgcdを取ります。今回はgcdがそのままmodulusとなりました。
#solver.py import math from Crypto.Util.number import * a = (中略) b = (中略) f = (中略) #f(31337) ff = (中略) #f(f(31337)) print(long_to_bytes(math.gcd(a*31337+b-f,a*f+b-ff)))
corctf{1n_m4th3m4t1c5,_th3_3ucl1d14n_4lg0r1thm_1s_4n_3ff1c13nt_m3th0d_
f0r_c0mput1ng_th3_GCD_0f_tw0_1nt3g3rs}
luckyguess
i hope you're feeling lucky today
nc be.ax 31800
添付ファイル:luckyguess.py
#luckyguess.py #!/usr/local/bin/python from random import getrandbits p = 2**521 - 1 a = getrandbits(521) b = getrandbits(521) print("a =", a) print("b =", b) try: x = int(input("enter your starting point: ")) y = int(input("alright, what's your guess? ")) except: print("?") exit(-1) r = getrandbits(20) for _ in range(r): x = (x * a + b) % p if x == y: print("wow, you are truly psychic! here, have a flag:", open("flag.txt").read()) else: print("sorry, you are not a true psychic... better luck next time")
線形合同法のような形でr回計算した値を予想します。rが20bitと小さい値だ、と思いましたが1/rを引くまで回すのは…。
x = ax + b mod p となるxを渡せば何回計算しようとも同じ値になります。
x = ax + b mod p (a-1)x = -b mod p x = -b/(a-1) mod p
#solver.py from Crypto.Util.number import * import socket # --- common funcs --- def sock(remoteip, remoteport): s = socket.socket(socket.AF_INET, socket.SOCK_STREAM) s.connect((remoteip, remoteport)) return s, s.makefile('rw') def read_until(f, delim='\n'): data = '' while not data.endswith(delim): data += f.read(1) return data HOST, PORT = "be.ax", 31800 p = 2**521 - 1 s, f = sock(HOST, PORT) a = int(read_until(f).split()[-1]) b = int(read_until(f).split()[-1]) x = ((p-b) * inverse(a-1,p))%p read_until(f,"point: ") s.send(str(x).encode()+b"\n") read_until(f,"guess? ") s.send(str(x).encode()+b"\n") flag = read_until(f).strip() print(flag)
corctf{r34l_psych1c5_d0nt_n33d_f1x3d_p01nt5_t0_tr1ck_th15_lcg!}
exchanged
you could make an exchange out of this
添付ファイル:exchanged.py, output.txt
#exchanged.py from Crypto.Util.number import * from Crypto.Cipher import AES from Crypto.Util.Padding import pad from hashlib import sha256 from secrets import randbelow p = 142031099029600410074857132245225995042133907174773113428619183542435280521982827908693709967174895346639746117298434598064909317599742674575275028013832939859778024440938714958561951083471842387497181706195805000375824824688304388119038321175358608957437054475286727321806430701729130544065757189542110211847 a = randbelow(p) b = randbelow(p) s = randbelow(p) print("p =", p) print("a =", a) print("b =", b) print("s =", s) a_priv = randbelow(p) b_priv = randbelow(p) def f(s): return (a * s + b) % p def mult(s, n): for _ in range(n): s = f(s) return s A = mult(s, a_priv) B = mult(s, b_priv) print("A =", A) print("B =", B) shared = mult(A, b_priv) assert mult(B, a_priv) == shared flag = open("flag.txt", "rb").read() key = sha256(long_to_bytes(shared)).digest()[:16] iv = long_to_bytes(randint(0, 2**128)) cipher = AES.new(key, AES.MODE_CBC, iv=iv) print(iv.hex() + cipher.encrypt(pad(flag, 16)).hex())
p = 142031099029600410074857132245225995042133907174773113428619183542435280521982827908693709967174895346639746117298434598064909317599742674575275028013832939859778024440938714958561951083471842387497181706195805000375824824688304388119038321175358608957437054475286727321806430701729130544065757189542110211847 a = 118090659823726532118457015460393501353551257181901234830868805299366725758012165845638977878322282762929021570278435511082796994178870962500440332899721398426189888618654464380851733007647761349698218193871563040337609238025971961729401986114391957513108804134147523112841191971447906617102015540889276702905 b = 57950149871006152434673020146375196555892205626959676251724410016184935825712508121123309360222777559827093965468965268147720027647842492655071706063669328135127202250040935414836416360350924218462798003878266563205893267635176851677889275076622582116735064397099811275094311855310291134721254402338711815917 s = 35701581351111604654913348867007078339402691770410368133625030427202791057766853103510974089592411344065769957370802617378495161837442670157827768677411871042401500071366317439681461271483880858007469502453361706001973441902698612564888892738986839322028935932565866492285930239231621460094395437739108335763 A = 27055699502555282613679205402426727304359886337822675232856463708560598772666004663660052528328692282077165590259495090388216629240053397041429587052611133163886938471164829537589711598253115270161090086180001501227164925199272064309777701514693535680247097233110602308486009083412543129797852747444605837628 B = 132178320037112737009726468367471898242195923568158234871773607005424001152694338993978703689030147215843125095282272730052868843423659165019475476788785426513627877574198334376818205173785102362137159225281640301442638067549414775820844039938433118586793458501467811405967773962568614238426424346683176754273 e0364f9f55fc27fc46f3ab1dc9db48fa482eae28750eaba12f4f76091b099b01fdb64212f66caa6f366934c3b9929bad37997b3f9d071ce3c74d3e36acb26d6efc9caa2508ed023828583a236400d64e
Diffie-Hellman鍵共有のような形で、shared = mult(A, b_priv) = mult(B, a_priv) となっており、これが分かればkeyを導出できAES暗号化されたflagを復号できます。A, Bは与えられていることから、a_priv or b_privを求めていきます。
mult関数を見ていきます。線形合同法のような計算をn(=a_priv or b_priv)回行います。nはかなり大きい数字のため、O(n)となる逐次処理では計算が終わりません。ゆえに、mult関数を高速化最適化を行います。
mult(s, 1) = as+b mod p mult(s, 2) = a(as+b) + b = (a^2)s +ab + b mod p mult(s, 3) = a((a^2)s+ab+b) + b = (a^3)s + (a^2)b +ab + b mod p -> mult(s, n) = (a^n)s + (a^(n-1))b + (a^(n-2))b + ... + ab + b = (a^n)s + b(((a^n)-1) / (a-1)) mod p
上記のように、規則性と等比数列の和の公式を使って高速化できる式となりました。ここからn(=a_priv or b_priv)を求めていきます。つまりnの式を作るよう変形すると、
mult(s, n) = A = (a^n)s + b(((a^n)-1) / (a-1)) mod p (a-1)A = (a^n)(a-1)s + (a^n)b - b mod p (as-a+b)(a^n) = (a-1)A + b mod p (a^n) = ((a-1)A+b) / (as-a+b) mod p
右辺は既知の変数のみで構成されているので計算できます。あとは、(右辺の値) = an mod pとなる値を求める過程だけなのですが、離散対数問題を解くということとなります。
p-1が素因数分解可能かつ小さい素数のみで構成されている場合、Pohlig-Hellman algorithmを用いて離散対数問題を解くことができます。
p-1を素因数分解してみると、小さい素数のみで構成されていたので、Pohlig-Hellman algorithmを使えそうです。
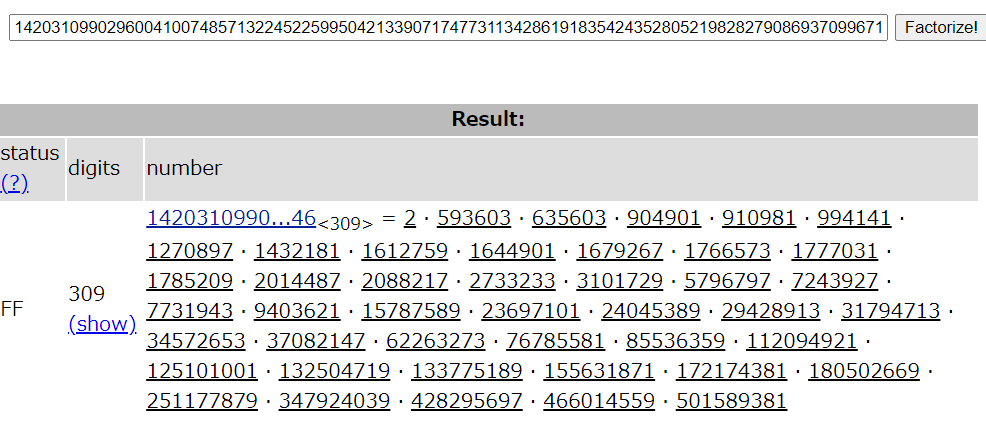
sageのdiscrete_logにはこのアルゴリズムが搭載されているようなので、あとはsageに任せます。
#sage 離散対数問題を解く print(discrete_log( Mod(右辺値, p), Mod(a, p) )
from Crypto.Util.number import * import math import gmpy2 from Crypto.Cipher import AES from Crypto.Util.Padding import pad from hashlib import sha256 p = (中略) a = (中略) b = (中略) s = (中略) A = (中略) B = (中略) enc = (中略) def mult(s, n): deno = inverse(a-1,p) t = ((pow(a,n,p)-1)*deno)%p return (pow(a,n,p)*s + b*t)%p An = ((A*(a-1)+b) * inverse((a-1)*s+b,p))%p Bn = ((B*(a-1)+b) * inverse((a-1)*s+b,p))%p print(An) print(Bn) #--- b_priv = 72294308363142635191285137067271613704518381689222403756427895774621470359587678998089163134800904011887080683864659561441585487866597353332892511005327144670737921076740544522591181991307617152388962472418690715521378068114703790176987564145359661515790454979281591952064634314009219343525018858317272168846 assert mult(s,b_priv) == B shared2 = mult(A, b_priv) print(shared2) key = sha256(long_to_bytes(shared2)).digest()[:16] iv = bytes.fromhex(enc[:32]) cipher = AES.new(key, AES.MODE_CBC, iv=iv) print(cipher.decrypt(bytes.fromhex(enc[32:])))
corctf{th1s_lcg_3xch4ng3_1s_4_l1ttl3_1ns3cur3_f0r_n0w}
hidE
This RSA encryption service is so secure we're not even going to tell you how we encrypted it
nc be.ax 31124
添付ファイル:main.py
#main.py #!/usr/local/bin/python import random import time import math import binascii from Crypto.Util.number import * p, q = getPrime(512), getPrime(512) n = p * q phi = (p - 1) * (q - 1) flag = open('./flag.txt').read().encode() random.seed(int(time.time())) def encrypt(msg): e = random.randint(1, n) while math.gcd(e, phi) != 1: e = random.randint(1, n) pt = bytes_to_long(msg) ct = pow(pt, e, n) return binascii.hexlify(long_to_bytes(ct)).decode() def main(): print('Secure Encryption Service') print('Your modulus is:', n) while True: print('Options') print('-------') print('(1) Encrypt flag') print('(2) Encrypt message') print('(3) Quit') x = input('Choose an option: ') if x not in '123': print('Unrecognized option.') exit() elif x == '1': print('Here is your encrypted flag:', encrypt(flag)) elif x == '2': msg = input('Enter your message in hex: ') print('Here is your encrypted message:', encrypt(binascii.unhexlify(msg))) elif x == '3': print('Bye') exit() if __name__ == '__main__': main()
UNIXTIMEの小数点以下を切り捨てた整数をシードとし、暗号化の要求があるたびに生成した乱数をeとしています(phiと互いに素でなければ、互いに素になるまで生成する)。flagの暗号文と任意の整数の暗号化を何回でも取得できます。
まず、シードは予測できそうです。ncするタイミングで±10秒あたりを見れば問題なさそうです。
eが1~nの間なので、かなり大きくなる可能性があるのでWiener's Attackかと思って進めていきましたが、e/nが0.96の場合でもうまくいかずdが小さくなってないのでしょう…。何かないかといつもの資料を見ていると、Common Modulus Attackなのでは?となりました。
www.slideshare.net
Common Modulus Attackは前半で出てくるイメージでしたが、だからといって気付くのが遅いなぁと反省。flagの暗号文を2つ取得し、シードをbrute forceして乱数を得てこの攻撃を行います。
#solver.py from Crypto.Util.number import * import socket import time import random import gmpy2 # --- common funcs --- def sock(remoteip, remoteport): s = socket.socket(socket.AF_INET, socket.SOCK_STREAM) s.connect((remoteip, remoteport)) return s, s.makefile('rw') def read_until(f, delim='\n'): data = '' while not data.endswith(delim): data += f.read(1) return data HOST, PORT = "be.ax", 31124 while True: try: tim = int(time.time()) s, f = sock(HOST, PORT) read_until(f) n = int(read_until(f).split()[-1]) print(f"n = {n}") for _ in range(5): read_until(f) read_until(f,"option: ") s.send(b"1\n") c1 = int(read_until(f).split()[-1],16) for _ in range(5): read_until(f) read_until(f,"option: ") s.send(b"1\n") c2 = int(read_until(f).split()[-1],16) for i in range(20): random.seed(tim) e_para = [] for k in range(100): e = random.randint(1, n) e_para.append(e) for i1 in range(len(e_para)-1): for i2 in range(i1+1,len(e_para)): e1 = e_para[i1] e2 = e_para[i2] g,s1,s2 = gmpy2.gcdext(e1,e2) g,s1,s2 = int(g), int(s1), int(s2) assert e1*s1 + e2*s2 == g if g == 1: m = (pow(c1,s1,n)*pow(c2,s2,n))%n flag = long_to_bytes(m) if b"corctf" in flag: print(flag) exit() tim += 1 except: pass
Wiener's Attackじゃないかと模索している間、この攻撃がpypiで実装されているのを発見して驚いてました(笑)
corctf{y34h_th4t_w4snt_v3ry_h1dd3n_tbh_l0l}
generous
Let me introduce you to this nice oracle I found...
nc be.ax 31244
添付ファイル:generous.py
#generous.py #!/usr/local/bin/python from Crypto.Util.number import getPrime, inverse, bytes_to_long from random import randrange with open("flag.txt", "rb") as f: flag = f.read().strip() def gen_keypair(): p, q = getPrime(512), getPrime(512) n = (p**2) * q while True: g = randrange(2, n) if pow(g, p-1, p**2) != 1: break h = pow(g, n, n) return (n, g, h), (g, p, q) def encrypt(pubkey, m): n, g, h = pubkey r = randrange(1, n) c = pow(g, m, n) * pow(h, r, n) % n return c def decrypt(privkey, c): g, p, q = privkey a = (pow(c, p-1, p**2) - 1) // p b = (pow(g, p-1, p**2) - 1) // p m = a * inverse(b, p) % p return m def oracle(privkey, c): m = decrypt(privkey, c) return m % 2 pub, priv = gen_keypair() n, g, h = pub print(f"Public Key:\n{n = }\n{g = }\n{h = }") print(f"Encrypted Flag: {encrypt(pub, bytes_to_long(flag))}") while True: inp = int(input("Enter ciphertext> ")) print(f"Oracle result: {oracle(priv, inp)}")
まずは中のアルゴリズムをまとめていきます。
暗号化 n = ppq h = g^n mod n c = g^m × h^r = g^m × (g^n)^r = g^(m+nr) mod n 復号 a = ((c^(p-1) mod p^2)-1) / p b = ((g^(p-1) mod p^2)-1) / p m = a × b^(-1) mod p oracle 公開鍵をくれる flagの暗号文をくれる 任意の暗号文を復号し、その下位1bitだけ教えてくれる
おそらくflagを1bitずつ求めていって復元するという形になると予想されます。
どっかで見たことあるなぁなんか名前あったなぁという暗号化方式で、自分の記憶を頼りにWaniCTFだったかなとはてなブログを遡ると…見つけました!
WaniCTF'21-spring Crypto Writeup - Attack All Around
暗号化方式は同じで復号oracleも存在しているのですが、この問題はflag以外の暗号文は全て復号してくれるという問題でした。cをflagの暗号文とすると、c' = c2 mod nを復号してもらうと2×flagとなり、半分で割ってlong_to_bytes()していました。それにしても、1年前の自分はちゃんと復号される証明までできていたのに今は分からなくて退化してる…。
この問題のflagより、この暗号化方式はOkamoto-Uchiyama cryptosystem(以後、OU)という名前のようです。
Okamoto–Uchiyama cryptosystem - Wikipedia
この名前でググるとほとんどCTFのwriteupなのですが、n=pppとしている問題かこのWaniCTFのものでした。
こちらのwriteupを参考にすると、OUは準同型暗号のようで平文x+yの暗号文はxの暗号文とyの暗号文の積となるようです。
それで2mの暗号文は、f(m+m) = f(m)×f(m) = c×c = c2 mod n なのかとようやく理解しました。OUCSはほとんどの方が、m+1の暗号文を作成してサーバに復号させていたようです。
以上より、m' = m//2 の暗号文をどうにか作れないかと式をたくさん書いた紙とにらめっこします。
m / 2 = m × 2^(-1) = m + m + ... + m mod n c' = c^(2^(-1)) mod n
このようにして、復号するとm/2となる暗号文c'を作成できました。しかしmが奇数である場合についても考える必要があります。mの下位1bitが分かれば次は2bit目です。1bit目が1である場合、(m-1)/2の暗号文を導出すれば2bit目が分かります。
(m-1)/2 = (m-1) × 2^(-1) = (m+(n-1)) × 2^(-1) = (m+(n-1)) + (m+(n-1)) + ... + (m+(n-1)) mod n c'' : (n-1)の暗号文 c'' = g^(n-1+nr) mod n c' = (c × c'')^(2^(-1)) mod n
cを復号して下位1bitが0ならm/2の暗号文を作り、下位1bitが1なら(m-1)/2の暗号文を作り、サーバによって暗号文を復号して下位1bitを得る。というのを繰り返してflagを復元していきます。
#solver.py from Crypto.Util.number import * import socket # --- common funcs --- def sock(remoteip, remoteport): s = socket.socket(socket.AF_INET, socket.SOCK_STREAM) s.connect((remoteip, remoteport)) return s, s.makefile('rw') def read_until(f, delim='\n'): data = '' while not data.endswith(delim): data += f.read(1) return data def make_flag(m): while len(m)%8: m += "0" m = int(m[::-1],2) print(long_to_bytes(m)) HOST, PORT = "be.ax", 31244 s, f = sock(HOST, PORT) read_until(f) n = int(read_until(f).split()[-1]) g = int(read_until(f).split()[-1]) h = int(read_until(f).split()[-1]) enc = int(read_until(f).split()[-1]) inv2 = inverse(2,n) n1enc = (pow(g,n-1,n)*pow(h,35,n))%n enc2 = (pow(g,inv2,n)*pow(h,35,n))%n flag = "" for i in range(1000): read_until(f,"ciphertext> ") s.send(str(enc).encode()+b"\n") ru = read_until(f) bits = ru.split()[-1] flag += bits if bits == "1": enc = (enc*n1enc)%n enc = pow(enc,inv2,n) make_flag(flag)
corctf{see?1_bit_is_very_generous_of_me}
corCTF 2021 : corCTF 2021 writeup - Attack All Around
leapfrog面白い問題なのですが、解けなくて悔しい…。
TFC CTF 2022 crypto writeup
皆さんご無沙汰しております。
前回writeupを書いたのが去年というのに驚いており、つまり今年初めてのwriteupとなっております。あけましておめでとうございます(?)
本題に入る前にこの7ヶ月間についてざっとお話ししたいと思いますが、解法を早く見たい方はスルーしてください(笑)
本当にざっとという感じになるのですが、なんだかんだ研究活動に勤しんでいました。加えてボウリングの方にも力を注いでいたため、土日にCTFをやる気力がなかったです…。3,4月は体調を崩しやすく(発熱してコロナかと思ったのに違ったのが2回)、研究への不安から身体面でも精神面でも余裕がなかった時期でした。
年内で大学でのCTF勉強会は一回区切りがつくこともありCTFから少し離れていたのですが、4月から新入生などの初心者勉強会や通常勉強会が始まり、問題集めのためちょっとずつ問題を解いていました。学会参加や修論発表が7月にあったのでそんなには取り組んでいませんでしたが、9月の卒業まで頑張っていこうと思います。
ちょっとした前説がありましたが、本題に入ります!
Official URL : https://ctf.thefewchosen.com/
warmup
OBSCURE
問題文をよく見ると奥の方にうっすらflagが…。

TFCCTF{s3cur1ty_thr0ugh_0bscur1ty}
BASIC
This guy keeps insulting my girlfriend! His last message confused me, though! Can you help me decode it?
/Rn/X7n#bUc.rjzh,|eEsg,?&QI;@^ARm}UKOkICi#X.ixEmN]D
何の暗号文か分からなかったので、cipher identifierを使ってbase91 encodeだと突き止めました。
Decrypt a Message - Cipher Identifier - Online Code Recognizer
あとはCyberChefやdcodeなど使ってdecodeです。
TFCCTF{sh3's_4_10..._but_0n_th3_ph_sc4l3}
MAFIOSO
A soldier was walking around the streets of Sicily, late at night, with THE Consigliere. Same soldier, the very next day, found in a ditch with a note in his breast pocket. It read:
f433c3e883a1389482c0b652660580f36ea037434fd4a67d193bc1cdc9b2cc34
Flag format: TFCCTF{secret_message}
この数値はなんだろう…。XORぽいが、だとするとflag formatからkeyのようなものを出しても、規則性は無い。"Consigliere", "Sicily" に関係する暗号も無い。
なんかあるかなと先ほどのcipher identifierを使ってみると、SHA-256の可能性があるとのこと。なるほど、数値の大きさをまず調べなかったのは反省。
ハッシュ値から元の値を特定するオンラインツールはいくつかありますが、中でもCrackStationは強い!
CrackStation - Online Password Hash Cracking - MD5, SHA1, Linux, Rainbow Tables, etc.
ここに投げて、出てきた文字列をTFCCTF{}で括って終わりです。この作業があるからflag formatをわざわざ出していたんですね。
TFCCTF{snitchesgetstitches}
easy
EXCLUSIVE ORACLE
"Hey! Let's keep all of our secrets together, in the same place!" "That's awesome, you're so friendly!"
Narrator: He wasn't friendly...
この問題が一番時間がかかりました…。easyと言えばそうかもしれませんが、エスパー要素が強め…?
今回のCTFは、ncする問題はCONTAINERを動かすよう指示する必要があり、その度にnc先が変わってしまいます。加えて、この問題ではnc先のサーバプログラムは公開していません。
とりあえずncしてみると、以下のようにdataを送ることができ、何かしらの暗号文が得られます。

何回かncして分かったこととして、
返ってくるバイト列の長さは、40+len(送ったdata)
ただし、len(送ったdata)が40を越えると、一律で長さ80となる
の二つだけです。
なんか40がくさいなということで、flagの長さだと予想します。
次に問題名よりXORを使うだろうということで、flagとkeyのXORが暗号文の最初40バイトと予想(←この仮定に至るまでかなり時間がかかった)。そして、暗号文の残りは自分の送ったdataも同じkeyでXORしているはず。keyの長さも40だとして、使いまわしているだろう。
data = 'a'×40として送り、暗号文後半40バイトとXORすることによりkeyを導出し、keyと暗号文前半40バイトとXORするとflagとなりました!
この問題のサーバを公開すればエスパー要素は無くなるけど、その分難易度がぐっと下がってしまう…。作問は難しいですね。
TFCCTF{wh4t's_th3_w0rld_w1th0u7_3n1gm4?}
medium
TRAIN TO PADDINGTON
The train to Paddington is leaving soon! Will you be able to find your ticket ID in time? Why did you encrypt it without storing the password...?
添付ファイル:main.py, output.txt
#main.py import os BLOCK_SIZE = 16 FLAG = b'|||REDACTED|||' def pad_pt(pt): amount_padding = 16 if (16 - len(pt) % 16) == 0 else 16 - len(pt) % 16 return pt + (b'\x3f' * amount_padding) pt = pad_pt(FLAG) key = os.urandom(BLOCK_SIZE) ct = b'' j = 0 for i in range(len(pt)): ct += (key[j] ^ pt[i]).to_bytes(1, 'big') j += 1 j %= 16 with open('output.txt', 'w') as f: f.write(ct.hex())
b4b55c3ee34fac488ebeda573ab1f974bf9b2b0ee865e45a92d2f14b7bdabb6ed4872e4dd974e803d9b2ba1c77baf725
長さ16のkeyを使いまわして、flagをpaddingしたものとXORしています。ここでのpaddingはb"\x3f" = b"?"を後ろに追加して16の倍数長になるようにしています。
flag formatから先頭7バイトが b"TFCCTF{" であることと、最後x(x : 1~16)バイトが b"}" + b"?"×(x-1) であることが分かります。ここからkeyをできるだけ特定していきます。xをbrute forceしてflagを一番復元できているものを見てみます。
#solver.py enc = "b4b55c3ee34fac488ebeda573ab1f974bf9b2b0ee865e45a92d2f14b7bdabb6ed4872e4dd974e803d9b2ba1c77baf725" key = [-1 for i in range(16)] flag_st = "TFCCTF{" for i in range(len(flag_st)): key[i] = ord(flag_st[i])^int(enc[i*2:(i+1)*2],16) for padlen in range(1,16): flag_ed = "}" + "?"*padlen tenc = enc[-32:] for j in range(16-len(flag_ed),16): key[j] = ord(flag_ed[j-16+len(flag_ed)])^int(tenc[j*2:(j+1)*2],16) print(f"pad length : {padlen}, ",end="") for i in range(len(enc)//2): if key[i%16] == -1: print("*",end="") else: c = key[i%16]^int(enc[i*2:(i+1)*2],16) print(chr(c),end="") print()
$ python3 solver.py
pad length : 1, TFCCTF{*******sn_h4s_l3*******1t4t10n}?*******}?
pad length : 2, TFCCTF{******v1n_h4s_l3******st4t10n}?******}??
pad length : 3, TFCCTF{*****041n_h4s_l3*****q_st4t10n}?*****}???
pad length : 4, TFCCTF{****6r41n_h4s_l3*****3_st4t10n}?****}????
pad length : 5, TFCCTF{***tr41n_h4s_l3***6h3_st4t10n}?***}?????
pad length : 6, TFCCTF{**q_tr41n_h4s_l3**th3_st4t10n}?**}??????
pad length : 7, TFCCTF{**3_tr41n_h4s_l3*6_th3_st4t10n}?*}???????
pad length : 8, TFCCTF{6h3_tr41n_h4s_l3$t_th3_st4t10n}?}????????
pad length : 9, TFCCTF9th3_tr41n_h4s_lqft_th3_st4t10n}}?????????
pad length : 10, TFCCTF{th3_tr41n_h4s_l3ft_th3_st4t10n}??????????
pad length : 11, TFCCG{th3_tr41n_h4sL.3ft_th3_st4t10}???????????
pad length : 12, TFC{th3_tr41n_h4>.3ft_th3_st4t1}????????????
pad length : 13, TFL{th3_tr41n_hx|.3ft_th3_st4t}?????????????
pad length : 14, TOML{th3_tr41n_a:|.3ft_th3_st4}??????????????
keyが全て復元できておらずXORできないものは"*"で表現しています。
ここから、flagが意味ある文章になるように特定できていないものをごちゃごちゃ頑張っていくのかなと思ったら、paddingの長さが10の時に完全復元できていました。
TFCCTF{th3_tr41n_h4s_l3ft_th3_st4t10n}
hard
ADMIN PANEL
This admin panel has been bugging me for days! It even lets me change the password and I can't log in!
添付ファイル:main.py
#main.py import os import random from Crypto.Cipher import AES KEY = os.urandom(16) PASSWORD = os.urandom(16) FLAG = os.getenv('FLAG') menu = """======================== 1. Access Flag 2. Change Password ========================""" def xor(byte, bytes_second): d = b'' for i in range(len(bytes_second)): d += bytes([byte ^ bytes_second[i]]) return d def decrypt(ciphertext): iv = ciphertext[:16] ct = ciphertext[16:] cipher = AES.new(KEY, AES.MODE_ECB) pt = b'' state = iv for i in range(len(ct)): b = cipher.encrypt(state)[0] c = b ^ ct[i] pt += bytes([c]) state = state[1:] + bytes([ct[i]]) return pt if __name__ == "__main__": while True: print(menu) option = int(input("> ")) if option == 1: password = bytes.fromhex(input("Password > ")) if password == PASSWORD: print(FLAG) exit(0) else: print("Wrong password!") continue elif option == 2: token = input("Token > ") if len(token) != 64: print("Wrong length!") continue hex_token = bytes.fromhex(token) r_byte = random.randbytes(1) print(f"XORing with: {r_byte.hex()}") xorred = xor(r_byte[0], hex_token) PASSWORD = decrypt(xorred)
まずmain.pyの挙動についてです。
1. Access Flag
入力した16進数をbytes型に変換し、それがPASSWORDと一致していたらflagを貰えます。何回でも実行可能です。
2. Change Password
長さ64となる16進数値を送り、bytes型に変換したものをtokenとします。サーバはそこから1byteの乱数値r_byteを生成&公開し、tokenの1byteごとr_byteでXORしていきます。その値をdecrypt関数に引数として渡し、その返り値をPASSWORDに置き換えます。
次にdecrypt関数についてです。引数として渡されるのは16進数で長さ64、つまり32バイトのものです。その前半16バイトをiv, 後半16バイトをctとします。
まずstate = ivとし、stateをAESのECBモードで暗号化した先頭1バイトをbとします。bとct[i]をXORしたものをptに追加します。そして、stateを先頭1バイトを取り除いたものとct[i]をつなげたものに更新します。ctの長さが16であることから、これを16回行った後のptを返します。
こちらも1. と同様、何回でも実行可能です。
つまりptは、[ivをAES暗号化した先頭1バイトとct[0]をXORしたもの] + [iv[1:]+ct[:1]をAES暗号化した先頭1バイトとct[1]をXORしたもの] + ... + [iv[15:]+ct[:15]をAES暗号化した先頭1バイトとct[15]をXORしたもの] となります。
KEYは分かる要素無いのに、どうやってAESで暗号化したものを特定するのか…。絶対無理やろ…。
ivとctが全部同じ1バイトで構成されていたら(ex. 464646...46)、stateをAES暗号化した先頭1バイトもct[i]もそれらをXORしたものも、この3つは必ず同じ値になります。つまり、ptは16進数で7b7b7b...7bというような形となります。送るtokenは1バイトごとr_byteでXORするので、全て同じ1バイトで構成すればこのようになります。
tokenをどのように設定してもptを完全に予測することはできませんが、上のようにすることでptを256通り("00"~"ff"×16)にまで絞ることができます。あとは、1. Access Flag で256通り全て試します(何回でも1. ができるのもミソ)。
#solver.py from Crypto.Util.number import * import socket # --- common funcs --- def sock(remoteip, remoteport): s = socket.socket(socket.AF_INET, socket.SOCK_STREAM) s.connect((remoteip, remoteport)) return s, s.makefile('rw') def read_until(f, delim='\n'): data = '' while not data.endswith(delim): data += f.read(1) return data #HOSTはIPアドレスでも可 HOST, PORT = "01.linux.challenges.ctf.thefewchosen.com", 59490 s, f = sock(HOST, PORT) for _ in range(4): read_until(f) read_until(f,"> ") s.send(b"2\n") read_until(f,"Token > ") s.send(b"35"*32+b"\n") read_until(f) for i in range(256): for _ in range(4): read_until(f) read_until(f,"> ") s.send(b"1\n") read_until(f,"Password > ") ans = hex(i)[2:] if len(ans) == 1: ans = "0"+ans s.send(ans.encode()*16+b"\n") flag = read_until(f).strip() print(i,flag) if "TFCCTF" in flag: break
TFCCTF{l0g0n_z3r0_w1th_3xtr4_st3ps!}
insane
ADMIN PANEL BUT HARDER (AND FIXED)
"This admin panel has been bugging me for days! It even lets me change the password and I can't log in!" But harder
添付ファイル:main.py
#main.py import os import random from Crypto.Cipher import AES KEY = os.urandom(16) PASSWORD = os.urandom(16) FLAG = os.getenv('FLAG') menu = """======================== 1. Access Flag 2. Change Password ========================""" def xor(bytes_first, bytes_second): d = b'' for i in range(len(bytes_second)): d += bytes([bytes_first[i] ^ bytes_second[i]]) return d def decrypt(ciphertext): iv = ciphertext[:16] ct = ciphertext[16:] cipher = AES.new(KEY, AES.MODE_ECB) pt = b'' state = iv for i in range(len(ct)): b = cipher.encrypt(state)[0] c = b ^ ct[i] pt += bytes([c]) state = state[1:] + bytes([ct[i]]) return pt if __name__ == "__main__": while True: print(menu) option = int(input("> ")) if option == 1: password = bytes.fromhex(input("Password > ")) if password == PASSWORD: print(FLAG) exit(0) else: print("Wrong password!") continue elif option == 2: token = input("Token > ") if len(token) != 64: print("Wrong length!") continue hex_token = bytes.fromhex(token) r_bytes = random.randbytes(32) print(f"XORing with: {r_bytes.hex()}") xorred = xor(r_bytes, hex_token) PASSWORD = decrypt(xorred)
先ほどのADMIN PANELの改良版ということで、サーバが生成する1バイトの乱数r_byteが、32バイトの乱数r_bytesと変更されています。同じようにやっても、全て同じバイトで構成されていないバイト列をdecrypt関数に送ることになり、ptを256通りに絞ることができません。
だったら、r_bytesを予想すればいいじゃないか!!!
r_bytesはrandom.randbytes()を利用しているので、その仕様を確認します。
def randbytes(self, n): """Generate n random bytes.""" return self.getrandbits(n * 8).to_bytes(n, 'little')
random.randbytes()はrandom.getrandbits()で得た数値をlittle endianでバイト列に変換し返します。
kurenaifさんがSECCON Beginners CTF 2022 "Unpredictable Pad" についての解法を掲載してくださっているので、そちらを参考にさせていただきました。
簡単に言うと、random.getrandbits()はメルセンヌ・ツイスターを利用しています。メルセンヌ・ツイスターは連続した624個の32ビット数値を得られるとその後の数値が予測できます。連続した312個の64ビット数値でも、[2個目の32ビット]+[1個目の32ビット] とすることで同様に予測できます。
kurenaifさんの解法より、randcrackを利用します。
GitHub - tna0y/Python-random-module-cracker: Predict python's random module generated values.
ここで、random.randbytes()はlittle endianで変換していることに注意します。kurenaifさんはおそらくbig endianの数値をrandcrackに投げているので、一度little endianからbig endianに戻します。そして、randcrackが予想した値をlittle endianに変換して、それを使って全て同じバイトで構成されているバイト列になるようtokenを調整すれば、後はADMIN PANELと同じです。
ADMIN PANEL BUT HARDER AND FIXEDも同じ解法です。
#solver.py from Crypto.Util.number import * import socket from randcrack import RandCrack # --- common funcs --- def sock(remoteip, remoteport): s = socket.socket(socket.AF_INET, socket.SOCK_STREAM) s.connect((remoteip, remoteport)) return s, s.makefile('rw') def read_until(f, delim='\n'): data = '' while not data.endswith(delim): data += f.read(1) return data #HOSTはIPアドレスでも可 HOST, PORT = "01.linux.challenges.ctf.thefewchosen.com", 60051 s, f = sock(HOST, PORT) rc = RandCrack() for i in range(624//8): print(f"i = {i}") for _ in range(4): read_until(f) read_until(f,"> ") s.send(b"2\n") read_until(f,"Token > ") s.send(b"35"*32+b"\n") ret = read_until(f).strip() ret = ret.split(": ")[1] rb = int.from_bytes(bytes.fromhex(ret),byteorder='little') while rb > 0: rc.submit(rb&((1<<32)-1)) rb >>= 32 pre_rb = hex(rc.predict_randrange(0, pow(2,256)-1))[2:] pre_rb = int.from_bytes(bytes.fromhex(pre_rb),byteorder='little') print(f"our prediction = {hex(pre_rb)[2:]}") val = int("35"*32,16) ret = val^pre_rb ret = hex(ret)[2:] while len(ret) < 32: ret = "0"+ret for _ in range(4): read_until(f) read_until(f,"> ") s.send(b"2\n") read_until(f,"Token > ") s.send(ret.encode()+b"\n") recv = read_until(f).split(": ")[1] print(f"result = {recv}") for i in range(256): for _ in range(4): read_until(f) read_until(f,"> ") s.send(b"1\n") read_until(f,"Password > ") ans = hex(i)[2:] if len(ans) == 1: ans = "0"+ans s.send(ans.encode()*16+b"\n") flag = read_until(f).strip() print(i,flag) if "TFCCTF" in flag: break
(HARDER) TFCCTF{n0_th3_fl4g_1s_n0t_th3_0ld_0n3_plus-Th3-w0rd_h4rd3r!}
(FIXED) TFCCTF{4pp4r3ntly_sp4ces_br34ks_th3_0ld_0ne}
おわりに
crypto全完ということもあり久しぶりにwriteupを書いてみました。前回からかなり間が空いたので、文章力が不安ではありますが、皆さんに伝わる内容だと幸いです。手ごたえのある問題があっての全完だったので結構嬉しかったです! これからも面白い問題の解きに書いていこうと思うので、読んでいただけると嬉しいです!
Harekaze mini CTF 2021 crypto writeup
official URL : Harekaze mini CTF 2021
終了後に解いて、3時間以内にcryptoは全完できたので自信になりました。全てのcryptoの問題について書けるのは久しぶりです。
writeup
ファイルなどは公式サイトからのDLをお願いします
first exam
kurenaif魔法学校の入学試験です。PythonでCrypto問を解く基礎を学んでください!
base64でencodeしたものをbytes_to_longして、さらに整数値keyとXORしており、その演算結果とkeyの値が渡されています。同じ値で2回XORすると元に戻る性質を使って、もう一度keyとXORしてlong_to_bytes → base64でdecodeでflagが復元されました。
import base64 from Crypto.Util.number import * key = 407773567691797768945309646881381330143924911048532252374484400956007416406007936505301187512369384531883020224488253602523154102140950477859193 flag = 1392812161183976577227166142672085037819799462496681473937900208451109718213256601589927195482395914799893761610554140977947503369343069077952836 flag ^= key print(base64.b64decode(long_to_bytes(flag)))
HarekazeCTF{OK_you_can_join_wizardry_school}
sage training
一緒にsageに入門しよう!
行列の演算を使ったRSAのようですね。
まず、2×2行列の2乗について考えます。
[ [a, b], [c, d] ] ^2 = [ [a*a + b*c, a*b + b*d], [c*a + d*c, c*b + d*d] ]
今回、対角成分はp, flagであり、それ以外は0となります。上記の例だと、b及びcが0となるので
[ [a, 0], [0, d] ] ^2 = [ [a*a + 0*0, a*0 + 0*d], [0*a + d*0, 0*0 + d*d] ] = [ [a*a, 0], [0, d*d] ]
と、対角成分だけが2乗されそれ以外の値は0になりました。同様に3乗, 4乗と計算しても同じ結果となるので、output.txtにある行列の対角成分は pe mod n, flage mod n となります。
前者(pe mod n)を使って素因数分解します。具体的には、この値はpの倍数かつnの倍数ではないことが分かっているので、gcdを取るとpの値が出てきます。
素因数分解ができたので秘密鍵dを求め、(flage)d mod nを計算すればflagとなります。SECCON CTF 2021 pppp のように行列をd乗して元通りにしても復元され、問題名よりこちらの方がより想定解なのかなと思っています。
from Crypto.Util.number import * import math c = [(94705679004463284733541288053549635663983624426348082883911423652044420589882644740030824857964094373277293351421545117172457918484063609288563394969114856228940330220982203798491227942337707868513380987219942847139213839127934175216087451584996193094098370176337671205679032479708240220775365041028562298045, 0), (0, 14243811671300968907609174458855708829741032120754409000357686908873126315334915231420353855815283498571171729689334442024813021199910238276500626386134036150649025606319036019223959715867658461585221634071508142818645594816357236002650041503442624594820852244903155433016041077813314542285538820574629698950)] n = 123658273021758657244926229590842169697216202161458868027271307824674005278002104678607018762498569110790554844101479136721968081586766904446085438475258864812618061595487772978115460674609635002737826341845366713797429237465562629770189347062332559337703309881797723858775511801114681134013841432780549606609 e = 65537 p = math.gcd(c[0][0],n) q = n//p phi = (p-1)*(q-1) d = inverse(e,phi) m = pow(c[1][1],d,n) print(long_to_bytes(m))
HarekazeCTF{which_do_you_like_mage_or_sage?}
mulmulmulti-prime rsa
Nが小さい素数がたくさんと、512bit素数2つの積となっています。この「小さい素数がたくさん」だけの総積はflagより大きいというのがミソでした。
まずNを素因数分解しようとfactorDBに投げると、397までの素数が1つずつと大きな合成数(=p×q)に分けることができます。そしてproblem.py内にプログラムでは使っていないのにcrt関数をimportしています。これが解法への誘導となっているとエスパーします。
ここで、素数の一つ7を例にとると、k = 2 mod 7 となる整数kについて、(k mod N) mod 7 も2となります。なんでかと言われるとなんとなく?となるのですごい方の証明を聞いてください…。
ゆえに、0~6をe乗した値を7で割った余りと0~6をe乗した値をNで割った余り(=暗号文c)をさらに7で割った余りは一致します。これを使うことで平文mを7で割った余りを特定することができます。これを素数2から397で同じことをして、中国剰余定理で平文を復元することができました。
from Crypto.Util.number import * from sympy.ntheory.modular import crt x = 397 num = 2 mod = [] val = [] c = 6444384937952479446360543800306726693252997452825552613901755375099255166714791921303820142603050845604453415771813934605436773362180219243666255359716995456217503120584807127945079526447091871683834669804927783277541340212953733681665967741288390917442432418885663222080013261671274096066346531406665749671823431928515791704387207382571496076159703188939522942673142857854899106254676400171188528066441584894129954980506317784944539407501773216256651827692873203651175 e = 65537 n = 13105434584967797009222723925714056612973229654650200307281518067540513311350491750775580308761120670043385919352137451528084580772272083564644136982142743585238409901075466075590932718136237274538943262152033321299508243379729042658808185056276914453786554308920681089647171956781340126500826872053436182017911021212882822071757885385543985492728290224139575551494811781675324350095354476279621406379090030101147754502075514438702852559140941288066281245455568260855730 while num <= x: if isPrime(num): mod.append(num) num += 1 for i in range(len(mod)): for j in range(mod[i]): if c%mod[i] == pow(j,e,mod[i]): val.append(j) break m, MOD = crt(mod,val) print(long_to_bytes(int(m)))
HarekazeCTF{Small_prime_numbers_give_a_large_amount_of_information}
lost key
秘密鍵も公開鍵も教えません。魔法学校に入門したならできますよね?
flagを1文字ずつRSAで暗号化していますが、公開鍵のNの方が未知です。しかしflag1文字のASCII値をe乗したものから暗号値を引くとNの倍数になります。これを分かっているflagの先頭12文字を利用して、Nの倍数を12個求めてgcdを取ると1024bitの値が出てきました。p, qは共に512bitであることから、この1024bitの値はNであると分かります。
以降は1回の暗号処理において平文が1byte分とかなり狭いので、平文をbrute forceすればflagが復元されます。
import math from Crypto.Util.number import * e = 65537 f = open("distfiles/output.txt") a = f.readlines() cs = eval(a[1][5:-1]) #print(type(cs)) flag_part = 'HarekazeCTF{' ncandi = ord('H')**e - cs[0] for i in range(1,len(flag_part)): ncandi = math.gcd(ncandi,ord(flag_part[i])**e - cs[i]) print('HarekazeCTF{',end="") for i in range(len(flag_part),len(cs)): for j in range(128): if pow(j,e,ncandi) == cs[i]: print(chr(j),end="") break print()
HarekazeCTF{Can_you_Recover_with0ut_the_public_4nd_pr1vate_keys!?}
m1z0r3CTF 2021 writeup
m1z0r3CTF 2021で作った問題の解説をしていきます。
その前に問題を見ていない方はこちらから:m1z0r3CTF 2021 作問しました - Attack All Around
解説
github URL : GitHub - ksbowler/m1z0r3CTF_2021: m1z0r3CTF 2021 problem files
15Prime (warmup)
flagを整数型に変換し、最下位ビットが立っていたら512ビットの素数を、立っていないなら256ビットの素数2つの積をoutput.txtに出力します。その後、その整数を1ビット右シフト、つまり2で割ります(余りは無視)。flagが0になるまで繰り返していきます。
つまり、出力された整数が素数なのか合成数なのか判断できればflagを復元できそうです。素数判定の関数はたくさんありますが、solverではlong_to_bytesも使うのでCrypto.Util.numberのisPrimeを使っています。output.txtに出力されている値はflagの下位ビットから見ているのに注意です。
from Crypto.Util.number import * f = open("output.txt") a = f.readlines() flag = "" for c in a: c = int(c.strip()) if isPrime(c): flag += "1" else: flag += "0" print(long_to_bytes(int(flag[::-1],2)))
m1z0r3{There_are_many_module5_that_1mplement_the_isprime_funct1on}
Long Island (easy)
flagからformatを除いたものを2進数表現した文字列をFLAG、31ビットの乱数を2進数表現した文字列をkeyとしてます。
ASCIIの可視文字列は7ビットで表現できるのに対し、1バイト分のメモリ(?)を確保しています。つまり、下から数えて8kビット目は必ず0になります。暗号文の長さが470であったことから、要素0から数えて8k+6番目のFLAGは必ず"0"になるので、その部分は暗号文とkeyが一致します("0" ^ key[i] = ciphertext[i] )。iが31を超えた場合、keyはi%31番目の値を使っています。つまりrotateして使っています。8ビット毎"0"が現れ、31と互いに素であり全てのkey[i]が一回は必ず"0"になる部分とXORします。これを用いてkeyを復元して暗号文から平文を導出します。
from Crypto.Util.number import * ct = eval(open("output.txt").read()) key = [] for _ in range(31): key.append(-1) for j in range(6,len(ct),8): key[j%31] = ct[j] #print(key) if min(key) >= 0: flag = "" for k in range(len(ct)): flag += str(key[k%31]^ct[k]) print(long_to_bytes(int(flag,2)))
m1z0r3{009->59->31_This_is_Seiya_Matsubara's_backnumber_transition}
1024Prime (medium)
まずRSA暗号の公開鍵と暗号文が渡されます。任意の暗号文を復号してくれるようなのですが、その復号された値について怪しげな演算をしているようです。
素数のうち小さいものから順に1024個を、配列に降順で格納しています。復号された値のビットと素数配列の要素を対応させ、立っているものと対応している素数を掛け合わせて1024で割った余りがサーバから送られてきます。
サーバから送られる値は1024で割った余りなので1024通りしかありません。復号された値は1024ビットなので、異なる復号値でも同じ値がサーバから送られてきてしまいます。また、その値から元の復号された値を復元するのは難しそうです。
しかし、1024個の素数の中でも異彩を放つのが"2"です。一つだけ偶数ですね。1024個の素数をどう掛け合わせようと、その中に2が含まれていたら偶数になります。2が対応しているのは復号された値の最下位ビットですね。偶数を偶数で割った余りなら必ず偶数になりますし、奇数なら必ず奇数が余りとなります。つまり、サーバから送られた値の偶奇を調べれば復号された値の最下位ビットが分かります。
この時、LSB Decryption Oracle Attackが使えます。
mを知りたいとき、復号すると2mになるような暗号文c'をサーバに送ります。c' = (2m)e = 2e × me = 2e × c mod nとなります。
c'を復号した際に2mがNを超えるかどうかを判断します。m < Nであるので、2m < 2Nとなります。つまり、復号された値 = 2m or 2m - N となります。前者の場合返り値は偶数で2mがNより小さいことが分かり、後者なら奇数となり2mがNより大きいことが分かります。ここで、0 < m < Nであった平文mの取りうる範囲が、0 < 2m < N, もしくは N < 2m < 2N の半分の候補となります。
一般化してみると、aN < km < (a+1)N (kは2のべき乗)という範囲が分かっているとします。この時、m' = km mod N = km - aN とし、2m'がNを超えるかチェックします。その確認は上記のやり方で行えばOKです。
2m'がNを超えない、0 < 2m' < Nの場合
0 < 2m' < N 0 < 2(km-aN) < N 0 < 2km - 2aN < N (ここですべての辺に2aNを足す) 2aN < 2km < (2a+1)N
とさらに、範囲を半分にすることができました。
反対に、2m'がNを超える場合、
N < 2m' < 2N N < 2(km-aN) < 2N N < 2km - 2aN < 2N (ここですべての辺に2aNを足す) (2a+1)N < 2km < (2a+2)N
とこちらの場合も範囲を半分にすることができました。
以上の操作を繰り返すと、aN < km < (a+1)N のkがかなり大きい値となります。a, k, m, Nは何れも整数なので、上の不等式を満たすmが一意に決まります。
細かい解説はgithubに載せた資料を参考にしてもらえればと思います。
from Crypto.Util.number import * from functools import reduce from operator import mul from itertools import combinations import sys import socket, struct, telnetlib # --- common funcs --- def sock(remoteip, remoteport): s = socket.socket(socket.AF_INET, socket.SOCK_STREAM) s.connect((remoteip, remoteport)) return s, s.makefile('rw') def read_until(f, delim='\n'): data = '' while not data.endswith(delim): data += f.read(1) return data #HOSTはIPアドレスでも可 HOST, PORT = "127.0.0.1", 5000 s, f = sock(HOST, PORT) e = int(read_until(f).split()[-1]) n = int(read_until(f).split()[-1]) c = int(read_until(f).split()[-1]) read_until(f) bounds = [[0,1],[1,1]] deno = 2 cnt = 0 while True: c2 = (pow(2,e,n)*c)%n read_until(f,"> ") s.send(str(c2).encode()+b"\n") ret = int(read_until(f).split()[-1]) bounds[0][0] *= 2 bounds[0][1] *= 2 bounds[1][0] *= 2 bounds[1][1] *= 2 if ret%2 == 0: #LSB 0 : 上限小さく bounds[0][0] += 1 else: #LSB 1 : 下限大きく bounds[1][0] -= 1 read_until(f) if cnt%100 == 0: print(cnt,bounds) if bounds[0] == bounds[1] or cnt > 1024: m = (n*bounds[0][0])//bounds[0][1] print(m) print(long_to_bytes(int(m))) break cnt += 1 deno *= 2 c = c2
m1z0r3{Did_you_know_LSB_Decrytion_Oracle_Attack}
SqUArE (hard)
Challenge S
e = 8750とp-1, q-1と互いに素ではないが倍数でもないという微妙な値。hintもその値がたまたま二乗根を持っていてあれ?となった方もいるかもしれません。
まず、p, qを求めます。
(p+q)^2 = p^2 + 2pq + q^2 = p^2 + q^2 mod pq
となりますが、なぜかこの値が二乗根をたまたま持っていました。私の想定する解法としては、p2 ≒ q2 ≒ pq と近似すると(p+q)2 = 4n+hintとなりそうです。なので、hintにnを足していって二乗根があるか調べて、あとは解と係数の関係でp, qを算出します。
次に、e = 8750という厄介な公開鍵をどうするか考えていきます。実はこの問題の値を変えただけです。
Buckeye CTF Defective RSA writeup - Attack All Around
計算すると28通りのmの候補が出てきますが、それをすべて見ると一つ怪しい文字列が…
Challenge U
公開鍵(e,n)と秘密鍵dが渡され、今のものよりも小さい秘密鍵が欲しいというワガママをかなえてあげましょう。
現状、ed = 1 mod (p-1)(q-1) で秘密鍵を作っているとのことなので、ed' = 1 mod lcm(p-1,q-1) にしてd'が小さくなればいいな戦法を取ります。では、どうやってe, n, dからp, qを求めるのかというと、ed-1が(p-1)(q-1)の倍数であることを使います。
ed-1 をfactorDBなどで素因数分解してビット全探査などを使い(p-1)(q-1)の候補を出します。正しい(p-1)(q-1)であれば、n-(p-1)(q-1) = p+q-1となるので、ここからまた解と係数の関係を利用しp, qを出します。あとは、lcmを計算してd'が小さくなればOK、ダメならもう一度ncするを繰り返すとうまくいきます。
渡された文字列がまたしてもFLAGじゃなかったですね…
Challenge A
AESのCBCモードを利用したログインサービスとのことです。
渡された暗号文をそのまま投げてみると、"guest"でログインできて"admin"じゃないから秘密のメッセージを渡せないと言われます。
渡された暗号文の最下位バイトを少し変えてみると、"Padding Incorrect"と言われました。
padding oracle attackに気づいたら、あとは実装のお時間です。
超絶分かりやすいサイトはこちら↓
Padding Oracle Attack 分かりやすく解説したい - Attack All Around
Decryption Attackにより以下の平文が手に入ったと思います。
SqUArE secret system: username = guest
暗号文をそのまま投げたら"guest"でログインできたので、その部分を"admin"にした暗号文を作ることができたら秘密のメッセージとやらを貰えそうです。
Encryption Attackを頑張って実装し、"admin"としてログインできると、またしてもFLAGじゃないものです。
Challenge E
私のgithubのサイトが得られたはずです。アクセスすると、chalE.py, outputE.txtがありました。
chalE.pyを読むと、m_list.txtには2進数で何かが格納されており、eをm_list.txtの行数ではなくm_list.txt内の異なる値の個数分でnは256ビット素数2つの積がe個ある、RSA暗号が使われていることが分かります。
1つの平文に対してe個の暗号文があるので、Hastad's broadcast attackを使えば平文を復号できます。
Coppersmith's attack - Wikipedia
復号してlong_to_bytesしても可視文字列になりません。それどころか\xffしかない平文もありました。しかし平文の長さが短いことから復号は間違ってないと思えるはずです。
ここからエスパー要素ふんだんに入っているのですが、勘のいい方はこの問題が最後だと気付いたと思います。問題名のSqUArEと今までのChallengeがS, U, A, Eであることから想像したのかなと思います。
chalE.pyの23行目からmが2進数で保存されているので2進数に変換すると、m_listの個数と各要素の長さが同じであることに気付きましたでしょうか。問題名のSqUArEから正方形にしてみたらなにか見えるはずです…。
SqUArEのq, rだけなぜ小文字なのでしょう。正方形でqとr…。加えて問題文…。
はい、QRコードです。
1を"##"に、0を"(空白2つ)"にして文字サイズを小さくすると端末でもQRコードが見えやすいと思います。あとはスマホのカメラかアプリなどで読み取ってもいいですし、PILなどを使って画像を生成してもいいと思います。
m1z0r3{sQuaRe_ha5_many_mean1ngs_maybe}
所感
学生最後のm1z0r3CTFということもあり、気合いを入れて多くの問題を作りました。SqUArEのChallenge Aはサーバコードすら見せないPadding Oracle Attackというのはかなりエスパーだったそうで、そこは反省しております。Challenge AをクリアしていないのにChallenge Eの問題を見れるようにはしたくなかったので、githubにコードを置くのはChallenge Eだけにしようと思っていました。もっといい方法があったのかな、など考えております。
また、Challenge Aは1024Primeで使ったLSB Decryption Oracle Attackにする予定でしたが、これはどうやってもサーバコードを見せないと分からないなとか、相手チームの問題数もまあまああると聞いて分断しました。全部RSAとなるのもつまらないかなと思ってAESを入れたのですが、内輪ネタ&チームメイトが他のAES問題を作問したのでもう少し改善できたのかなと思っています。
SqUArEはボス問のような形にしたくて簡単には解かれたくなかったので(特に相手チームのsiro君には) Challenge 4つ構成にしましたが、1人が8時間かけてギリギリ解けないというかなり鬼畜設定にしすぎました。最後のQRコード変換はWebの問題をやったときに体験して自分も作ってみたいと思っていました。
もう一つ物議をかもした問題がLong Islandです。これが初心者用問題にはならんやろ!とお𠮟りを受けました。チーム内でもASCIIの8ビット毎に必ず0になるというのに気付く人はいなくて言われたら気付くという意見を貰いましたが、そのまま出題。見事(?)解かれませんでした。この問題は、布団に入ったはいいものの眠れなかった日に構想していたものです。
余談ですが、巨人松原選手が2022年シーズンにまた新しい背番号9になることが発表されました。プロ野球界では一桁背番号はかなり期待されている選手や主力が付ける傾向があり、巨人の背番号9は2021年引退した亀井選手が付けていました。今後の松原選手の活躍に期待ですね!
SECCON CTF 2021 writeup
official URL : SECCON CTF 2021
pppp
Great research on witch has made it possible to split and duplicate messages.
ファイル : problem.sage, output.txt
# problem.sage from Crypto.Util.number import * from flag import flag p = getStrongPrime(512) q = getStrongPrime(512) n = p*q mid = len(flag) // 2 e = 65537 m1 = int.from_bytes(flag[:mid], byteorder='big') m2 = int.from_bytes(flag[mid:], byteorder='big') assert m1 < 2**256 assert m2 < 2**256 m = [[p,p,p,p], [0,m1,m1,m1], [0,0,m2,m2],[0,0,0,1]] # add padding for i in range(4): for j in range(4): m[i][j] *= getPrime(768) m = matrix(Zmod(p*q), m) c = m^e print("n =", n) print("e =", e) print("c =", list(c))
#output.txt n = 139167515668183984855584233262421636549219808362436809125322963984953234794207403032462532211718407628015534917936237180092470832870352873174416729863982860547330562153111496168661222608038945799305565324740297535609102402946273092600303759078983973524662838350143815732516927299895302494977521033451618509313 e = 65537 c = [(92641859227150025014514674882433433169736939888930400782213731523244191029744271714915087397818608658221982921496921528927873080896272971564627162670330785041427348269531449548757383647994986600796703130771466176972483905051546758332111818555173685323233367295631863710855125823503925281765070200264928761744, 1077078501560459546238096407664459657660011596619515007448272718633593622581663318232822694070053575817000584000976732545349394411037957356817674297166036371321332907845398174111343765006738074197964396832305908342965034091516961317164203682771449331094865994143953470394418754170915147984703343671839620070, 19878161032897109459692857500488708331148676837923170075630073845924376353394086221031683671854185288619608305138965881628353471119235227157715699650190844508727073649527735233175347600167954253143204293274253676829607434380971492999430389536409563073620686264607716424139208756197843637115228155976163983619, 122958657434560838063916316490126514822437273152981380647634868499620566657448363565613345650206126542999322277498960954804580159527199119604554047697342524367459283765958189416627623253226055220105627822118413649499651442079969872322463271891353808314530249098525814619479135297014148780695960117897387220659), (0, 85635304452753185796593135650704585992713419302092444931829191186284566226617686976975731459756968679710078670232999566062343743901469759277582454092882685887985731708244015567469990157564460035983017331880588783841581502687752495254387549274422591338211161917565559735193456411356422539814020979699927207024, 26528377397409932803048052918715873209845190225305139460936852681030879561522825277119360099719008486268731610926098705442795761739644784858085976938906030639986454157616558457541083641717564142619063815917161350343604401278251069255966146207538326575595944701499010180658631016268689550402326369924649514049, 17173480018007185616783556851363148729840100207266610547324632027095687866456613104465211034834604995290825437734467654701021261504226847008483339028335703977866796341754911432666568936460974103742649586111260163432789617417125379644939110280618415377202845096157056174169392363954229816964869557167190373166), (0, 0, 81417110160690915414859599923077760437964436481940074249510026432592954854440295980578313776441414052192070135409849396229653279814546498083873720679422968334818254076803899882280264290639872486915551889441082468560654475422089052988909565455596584407805229280743723696618903551087160338683566908533474596220, 88524270641123978066493517684012199807956329430551155649688209766850898125045959831704501988313531767120589113923546449704920649814085765896894870692227804052901254644766662594723181025793077392532746071480212649880063471693730914835259139038459097504431147211622052068997412540488201406879310193174863792764), (0, 0, 0, 130146806238985078905344376697263038970354607413027156915068014483770022716717215156189413217688976902906182579031431264733207976605553885314360422441780388319618199732296392330859801016851191010568169307878720202422104375360360029207688301496478751250969744747470242179561459045172707909287093959859681318497)]
上三角行列をe乗しているようです。上三角行列ってe乗すると、対角成分は元の行列の対角成分をe乗した値になるんですね。これで、(x11×p)e, (x22×m1)e, (x33×m2)e, (x44)e (全てにmod n) が対角成分であることが分かりました(xij はgetPrime(768)で得られる素数)。(x11×p)e mod n はpの倍数かつnの倍数ではないのでgcd取ればnを素因数分解できます。そしてそこから秘密鍵を求めて、x22×m1, x33×m2を導出しました。
ここからどうしよう、となりとりあえずfactorDBに投げるとどちらも768bitの素数とその他になるような素因数分解はできませんでした。素因数分解できなかった値のbit長を見てみると835, 881ともうちょっとがんばったら素因数分解できそう(自分じゃできない)と思いsageに投げるもダメ。チームメイトに他に素因数分解してくれるサイト知らない?と聞くとこちらを教えてくれました。
Integer factorization calculator
x22×m1の素因数分解は5分程でできたので、x33×m2もすぐか?と思いましたが結局9時間かかりました。けど開始9時間以内に解いているチームもあったので、これは想定解ではないようです。
結局、あの行列をd乗すれば元に戻るみたいです。なんで? そこからx22×m1とx23×m1をgcd取ればm1が出てきて同じ方法でm2も算出できるみたいです。
SECCON{C4n_y0u_prov'b'e_why_decryptable?}
cerberus
Cerberus is guarding a secret text.
nc cerberus.quals.seccon.jp 8080
ファイル:problem.py
#problem.py import base64 from Crypto.Cipher import AES from Crypto.Random import get_random_bytes from Crypto.Util.Padding import pad, unpad from Crypto.Util.strxor import strxor from flag import flag import signal key = get_random_bytes(16) block_size = 16 # encrypt by AES-PCBC # https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation#Propagating_cipher_block_chaining_(PCBC) def encrypt(m): cipher = AES.new(key, AES.MODE_ECB) # MODE_PCBC is not FOUND :sob: :sob: m = pad(m, 16) m = [m[i : i + block_size] for i in range(0, len(m), block_size)] iv = get_random_bytes(16) c = [] prev = iv for m_block in m: c.append(cipher.encrypt(strxor(m_block, prev))) prev = strxor(c[-1], m_block) return iv, b"".join(c) # decrypt by AES-PCBC # https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation#Propagating_cipher_block_chaining_(PCBC) def decrypt(iv, c): cipher = AES.new(key, AES.MODE_ECB) # MODE_PCBC is not FOUND :sob: :sob: c = [c[i : i + block_size] for i in range(0, len(c), block_size)] m = [] prev = iv for c_block in c: m.append(strxor(prev, cipher.decrypt(c_block))) prev = strxor(m[-1], c_block) return b"".join(m) # The flag is padded with 16 bytes prefix # flag = padding (16 bytes) + "SECCON{..." signal.alarm(3600) ref_iv, ref_c = encrypt(flag) print("I teach you a spell! repeat after me!") print(base64.b64encode(ref_iv + ref_c).decode("utf-8")) while True: c = base64.b64decode(input("spell:")) iv = c[:16] c = c[16:] if not c.startswith(ref_c): print("Grrrrrrr!!!!") continue m = decrypt(iv, c) try: unpad(m, block_size) except: print("little different :(") continue print("Great :)")
PCBCモードなるものがあるんですね。unpadが成功したかどうかでサーバから送られる文字列が変わるのでPadding Oracle Attackのようです。
Padding Oracle Attack 分かりやすく解説したい - Attack All Around (最近こちらの記事がよく読まれているようで感謝しかありません)
けどこれはCBCモードとは異なり、暗号文と平文のxorがkeyによってdecryptされた値とxorしています。なので暗号文を変えてPadding Oracle Attackをしようとすると、それに対応する平文も変わりxorされる値がごっちゃになります。かつ問題ファイルにあるif文から貰った暗号文から始まる暗号文でないとdecryptしてくれないようです。そこで、ivを変えてPadding Oracle Attackすることを思いつきますが、その値をどうしたらいいのだろうとなりタイムアップ…。
暗号文は64バイトであることから4ブロックあることが分かります。それぞれc0, c1, c2, c3とすると、c0~c3+c3を送った際の第4ブロック(1つ目のc3)の復号でdec(c3)とxorする値をAとします。第5ブロック(2つ目のc3)の復号処理が終わると、その平文ブロックと暗号文ブロックをxorするとAになります。
p3 = A xor dec(c3) p4 = dec(c3) xor c3 xor p3 = dec(c3) xor c3 xor A xor dec(c3) = c3 xor A c3 xor p4 = c3 xor c3 xor A = A
同様に、c0~c3+c3+c2を送ると、最後の平文及び暗号文ブロックをxorした値は第3ブロック(1つ目のc2)の復号でdec(c2)とxorする値と同じになります。
これを繰り返して考えます。c0~c3+c3~c0を送ると、最後の平文及び暗号文ブロックをxorした値はivとなります。c0~c3+c3~c0+c0を送ると、最終ブロックの復号処理でこちらが送ったivとdec(c0)をxorした値が最終平文ブロックとなります。Padding Oracle Attackで最終平文ブロックがb"\x10"*16となるよう頑張ってivを変えていくと、dec(c0)の値が分かります。それを元のivとxorするとp0が分かります。以降piを求める場合、dec(ci)の値を求めて元のIVではなくc(i-1)とp(i-1)をxorした値とxorすればOKです。
SECCON{v._.^v-_-v^._.^_S0und_oF_0rpHeUs_Aha~~}
個人的CTFで面白かったchallengeまとめ
学生卒業まで1年を切ったので、今までの集大成を記録していきたいと思います。(随時更新予定)
Classical Cryptography
picoCTF 2021 New Caesar
picoCTF 2021 writeup - Attack All Around
picoCTF 2021 New Vignere
picoCTF 2021 writeup - Attack All Around
Original Cryptography
SunshineCTF 2020 Magically Delicious
SunshineCTF 2020 Magically Delicious writeup - Attack All Around
ångstromCTF 2021 Home Rolled Crypto
ångstromCTF 2021 writeup - Attack All Around
Mathematics
Harekaze mini CTF 2021 mulmulmulti-prime rsa
Harekaze mini CTF 2021 crypto writeup - Attack All Around
K3RN3L CTF Pascal RSA
CTFtime.org / K3RN3LCTF / Pascal RSA / Writeup
Crypto CTF 2019 Alone in the dark
隣り合うピタゴラス数の証明 Crypto CTF 2019 Alone in the dark - Attack All Around
Cyber Apocalypse CTF 2021 Little Nightmares
リンク無しですごめんなさい。
WaniCTF 21 Spring OUCS
WaniCTF'21-spring Crypto Writeup - Attack All Around
DawgCTF 2021 TrashChain
DawgCTF 2021 writeup - Attack All Around
hsctf 8 agelaius-phoeniceus
hsctf 8 writeup - Attack All Around
ImaginaryCTF 2021 Primetime
ImaginaryCTF 2021 Writeup - Attack All Around
RSA
InterKosen CTF 2020 ciphertexts
InterKosenCTF 2020 ciphertexts writeup - Attack All Around
TokyoWesterns CTF 6th 2020 twin-d
TokyoWesterns CTF 6th 2020 一問も解けなかった話 - Attack All Around
Buckeye CTF Defective RSA
Buckeye CTF Defective RSA writeup - Attack All Around
picoCTF 2021 It's Not My Fault 1
picoCTF 2021 writeup - Attack All Around
Plaid CTF 2021 XORSA
Plaid CTF 2021 XORSA writeup - Attack All Around
SECCON Beginners CTF 2021 p-8RSA
SECCON Beginners CTF 2021 Crypto writeup - Attack All Around
CryptoHack
問題URL : CryptoHack – RSA challenges
Null or Never
AES
SECCON CTF 2021 cerberus
SECCON CTF 2021 writeup - Attack All Around
ångstromCTF 2021 Oracle of Blair
ångstromCTF 2021 writeup - Attack All Around
DawgCTF 2021 What the Filp?!
DawgCTF 2021 writeup - Attack All Around